Trong Toán học có một bài toán đã trở nên cực kì quen thuộc đối với bất cứ ai trong chúng ta, đó là bài toán ba đường trung tuyến của tam giác. Bài toán ba đường trung tuyến là một bài toán có hấp lực vô cùng lớn. Đứng về phương diện hình học Afin nó là một trong những bài toán Afin đơn giản nhất. Đứng về phương diện Hình học Euclide nó là một bài toán có sức phát triển rất cao mà hết cả cuộc đời chúng ta không bao giờ đi tới tận cùng của nó. Vẻ đẹp của mối quan hệ giữa Hình học sơ cấp và Hình học cao cấp, đó là nét đẹp giữa cái đơn giản và phức tạp là mối quan hệ nhiều chiều mà ta cần quan tâm. Xin được chia sẻ với các bạn về những điều đã nói trước hết qua bài toán sau :

ĐẾN VỚI BÀI TOÁN CÓ NHIỀU CÁCH GIẢI - P1

Trước khi đến với cách giải tiếp theo, ta hãy đến với một số khái niệm về trọng tâm.

1. Khái niệm trọng tâm

1.1 Định nghĩa 1Trọng tâm (tâm tỉ cự) hai chất điểm (A, a) và (B, b) là điểm thứ ba (C) nằm trên AB và thoả mãn quy tắc đòn bẩy : Tích các khoảng cách từ một trong hai điểm đã cho, ví dụ điểm A với khối lượng tại điểm đó (a) bằng tích của khoảng cách từ nó đến điểm còn lại B với khối lượng đặt tại điểm đó (b) : a . AC = b . BC.

Tâm tỉ cự hai chất điểm A = (A, a) và B = (B, b) có thể kí hiệu là Z(A, B).

1.2 Định nghĩa 2Tâm tỉ cự (hay trọng tâm, hay tâm khối) của n chất điểm A₁ = (A₁, m₁), A₂ = (A₂, m₂), …, A_n = (A_n, m_n) với n > 2 là một điểm có được nhờ cách sau :

1) Tìm tâm tỉ cự C_{n – 1}của n – 1 chất điểm A₁, A₂, …, A_{n – 1}.

2) Điểm C_n được định nghĩa là tâm tỉ cự của hai chất điểm : C_{n – 1} = (C_n, m₁+ m₂ + … + m_{n – 1}) và A_n = (A_n, m_n).

Nếu tồn tại tâm tỉ cự C_ncủa hệ n chất điểm : (A₁, m₁), (A₂, m₂), …, (A_n, m_n), ta đặt toàn bộ khối lượng của hệ đó tức là khối lượng m₁ + m₂ + … + m_n thì chất điểm được tạo thành như vậy (C_n, m₁ + m₂ + … + m_n) gọi là tâm vật chất của hệ điểm đã cho.

1.3. Các tính chất

1) Đối với mọi hệ chất điểm, tâm tỉ cự luôn luôn tồn tại duy nhất.

2) Vị trí tâm tỉ cự của hệ không phụ thuộc vào thứ tự kết hợp liên tiếp các điểm đó.

3) Vị trí tâm tỉ cự của hệ chất điểm không thay đổi nếu thay một số điểm của hệ bằng tâm vật chất của nó.

Cách 11 (Sử dụng khái niệm trọng tâm)

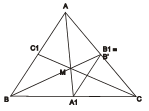
Đặt (A, 1), (B, 1) thì tâm tỉ cự (A, B) là (C₁, 2), đặt (C, 1). Khi đó trọng tâm hệ (C, C₁) là M mà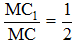

Nối BM cắt AC tại B₁, AM cắt BC tại A₁. DO tâm tỉ cự của hệ ba điểm A, B, C tồn tại duy nhất. Suy ra A₁ là trung điểm của BC, B₁ là trung điểm của AC.

Trước khi đến với cách giải tiếp theo, ta hãy đến với một số kết quả của Vật lý sau :

2. Một số tiên đề về lực

Các khái niệm mở đầu :

a) Lực là đại lượng vectơ đặc trưng cho tác dụng , tương hỗ của các vật.

b) Vật rắn tuyệt đối là vật không có khả năng biến dạng , tức có kích thước và hình dáng không đổi (dưới đây chỉ nói đến vật rắn tuyệt đối).

c) Hệ lực cân bằng là hệ lực khi đặt vào vật đứng yên thì không gây ra chuyển động của vật đó.

d) Hai hệ lực tương đương là hai hệ lực gây ra tác dụng như nhau khi đặt vào cùng một vật.

e) Hợp lực của hệ lực là một lực tương đương với hệ lực đó.

Tiên đề 1Điều kiện cần và đủ để hai lực cân bằng là chúng có cùng độ lớn , cùng đường tác dụng và ngược hướng.

Tiên đề 2Nếu thêm vào hoặc bớt đi ở hệ lực đã cho hai lực cân bằng sẽ được hệ lực tương đương với hệ lực đã cho.

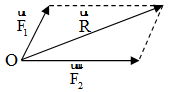
Tiên đề 3Hợp lực 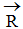của hai lực 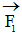và 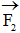đặt vào một điểm O được biểu diễn bởi đường chéo của hình bình hành mà hai cạnh là hai lực , .

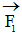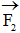Hệ quả 1Từ hai tiên đề đầu, suy ra rằng tác dụng của lực lên vật rắn không đổi nếu ta dời điểm đặt của lực trên đường tác dụng của nó.

Thật vậy, cho lực 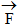đặt tại A. Đặt thêm vào B hai lực cân bằng 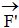và với F’ = F. Ta có theo tiên đề 2: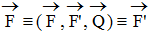

Như vậy có thể coi là lực F đặt tại A đã dời về B.

Hệ quả 2Từ các tiên đề 1, 3 và hệ quả 1, suy ra : Nếu ba lực không cùng song song nằm trong một mặt phẳng mà cân bằng thì chúng phải đồng quy.

Thật vậy, theo giả thiết các đường tác dụng của lực phải cắt nhau. Gọi hai lực có đường tác dụng cắt nhau l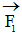à và 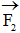. Dời các lực này về giao điểm O của chúng và hợp lại theo tiên đề 3 ta được một lực 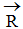đặt tại O. Muốn lực còn lại 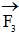cân bằng với 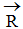thì lực 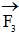cũng phải đi qua O (theo tiên đề 1).

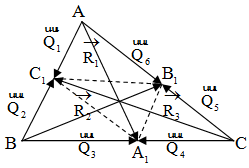
Cách 12 Ta đặt vào các đỉnh của tam giác, sáu lực từng đôi một cân bằng. Ta có :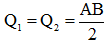

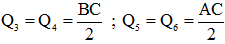
Hợp lực của các cặp lực nằm trên những đường trung tuyến cũng phải cân bằng và do đó theo hệ quả 2, chúng phải đồng quy.

Cách 13 (Phương pháp Giải tích)

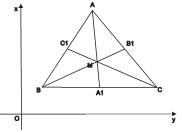
Xét hệ trục tọa độ vuông góc Oxy như hình vẽ. Giả sử A(x₁ ; y₁) ; B(x₂; y₂) ; C(x₃ ; y₃). Gọi M là điểm có tọa độ 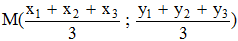. Ta cần chứng minh AM, BM, CM cắt các cạnh đối diện tại trung điểm của mỗi đường.

Gọi A₁là trung điểm của BC ; A₁ có tọa độ là : .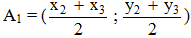

Ta có :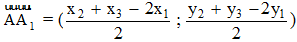

Ta có :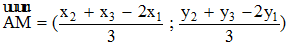

Vậy 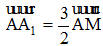. Hay A, M, A₁ thẳng hàng.

Lập luận tương tự ta cũng có : B, M, B_­1 thẳng hàng và C, M, C₁ thẳng hàng.

Hay ba đường trung tuyến đồng quy tại một điểm.

Cách 14 (Phương pháp Giải tích)

Xét hệ trục toạ độ Afin mà trục hoành nhận 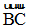làm vectơ đơn vị, trục tung 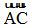là vectơ đơn vị, gốc là B.

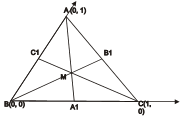
Lúc đó A, B, C có tọa độ là : A (0, 1) ; B(0, 0) ; C(1, 0) và tọa độ các trung điểm A₁, B₁, C₁ là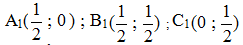

Phương trình AA₁, CC₁, BB₁ lần lượt là :

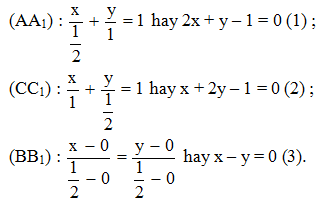
Ta chứng minh CC₁, BB₁, AA₁ đồng quy như sau :

Gọi M(x ; y) là giao điểm của AA₁và CC₁, tọa độ (x ; y) của M là nghiệm của hệ phương trình:

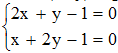
Trừ vế theo vế ta có tọa độ (x ; y) của M nghiệm đúng hệ phương trình : x – y = 0. Hay M thuộc đường thẳng BB₁. Do đó ba đường thẳng AA₁, BB₁, CC₁ đồng quy.

Trước khi đến với cách giải sau ta hãy đến với định lý sau trong hình học Xạ ảnh :

3. Định lý 1Điều kiện cần và đủ để Ax, By, Cz đồng quy (ABC là một tam giác) là các cặp tia xuất phát từ một điểm O nào đó và theo thứ tự song song với cặp (Ax, BC), (By, CA), (Cz, AB) là ba cặp tia tương ứng của một phép đối hợp.

Từ định lý này, ta có cách giải sau :

Cách 15 Ta chọn là đường trung bình nối hai trung điểm C₁, B₁ của hai cạnh AB, AC.

Ax, BC cắt ở điểm chính giữa L của đoạn C₁B₁ và ở điểm vô tận tức là hai điểm chia điều hòa C₁, B₁.

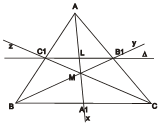
By, CA cắt ở hai điểm trùng nhau ở B₁.

Cz, AB cắt ở hai điểm trùng nhau ở C₁.

Ba cặp (L,), (C₁, C₁), (B₁, B₁) quả là ba cặp điểm tương ứng của một phép đối hợp. Vậy ba trung tuyến đồng quy.

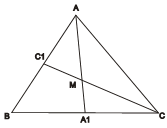
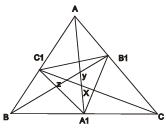Cách 16Giả sử những đường trung tuyến AA₁, BB₁, CC₁ trong tam giác ABC không cắt nhau tại một điểm (hình vẽ). Khi đó chúng đôi một cắt nhau thành ba điểm X, Y, Z không nằm trên một đường thẳng. Ta thấy rằng tam giác XYZ nằm trong tam giác ABC. Nối trung điểm của các cạnh tam giác ABC ta nhận được tam giác A₁B₁C₁. Đoạn thẳng B₁C₁ là đường trung bình của tam giác ABC nên C₁B₁ // BC. Kí hiệu A₂ là giao điểm của AA₁với C₁B₁. Theo định lý Talet, AA₂ = A₂A₁, vì thế

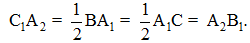
Như vậy đoạn thẳng A₁A₂là đường trung tuyến của tam giác A₁B₁C₁. Chứng minh tương tự những đường trung tuyến còn lại của tam giác A₁B₁C₁cũng là những đường trung tuyến của tam giác ABC. Vì thế tam giác XYZ cũng nằm trong tam giác A₁B₁C₁. Nối trung điểm các cạch của tam giác A₁B₁C₁ ta nhận được tam giác A₂B₂C₂(hình vẽ), mà trung tuyến của nó cũng là trung tuyến của tam giác A₁B₁C₁(nghĩa là của tam giác ABC, vì thế tam giác XYZ cũng nằm trong tam giác A₂B₂C₂và tiếp tục quá trình này.

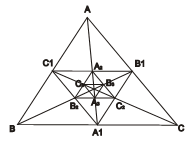
Ta nhận được dãy những tam giác ABC, A₁B₁C₁, A₂B₂C₂, …, A_nB_nC_n … đều chứa trong mình tam giác XYZ. Theo tính chất độ dài trung bình của tam giác ta có

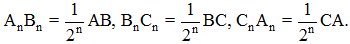
Dùng tính chất hình đồng dạng về diện tích, ta có

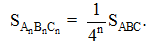
Từ đó suy ra

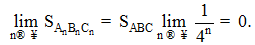
Vì thế bằt đầu từ một số n nào đó 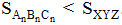Điều này vô lí, nghĩa là ba đường trung tuyến phải giao nhau tại một điểm. Ta kí hiệu giao điểm đó là P, và độ dài đường trung tuyến là AA₁ = m.

Khi đó AP = AA₂ + A₂A₄ + A₄A₆+ … Nhưng vì 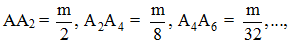suy ra

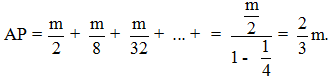
Điểm P đã chia trung tuyến theo tỉ lệ 2 : 1.

Từ một bài toán quen thuộc nhưng chúng ta đã có nhiều cách nhìn đa chiều. Từ hình học Euclide đến hình học Afin, Xạ ảnh. Từ sơ cấp cho đến cao cấp. Đó là một mối quan hệ tuyệt đẹp giữa các phương pháp với nhau. Hy vọng với bài viết này sẽ đem đến cho các bạn nhiều điều hay và thú vị. Chúc các bạn thành công trong cuộc sống!